Hace poco hablábamos de los DGGS (Discrete Global Grid Systems) o Sitemas de Mallas Globales y Discretas, un nueva Especificación Abstracta del OGC que puede que cambie el cómo georreferenciamos nuestros datos y que quizás suponga un adios a los clásicos Sistemas de Referencia por Coordenadas. (Véase esta entrada).
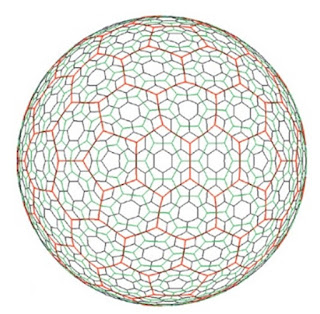
Hemos visto algunos detalles adicionales curiosos y vamos a resumirlos aquí. Por un lado, hay teselaciones de cuasiexágonos que recubren la esfera empaquetándose en varios niveles que resultan atractivas:
otros sistemas rotan cada celdilla hexagonal al pasar de un nivel de resolución a otro:
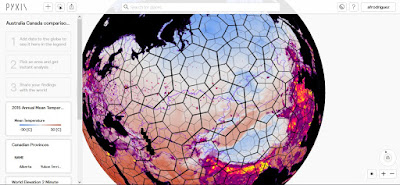
como el que emplea la empresa canadiense PYXIS en la implementación que puede verse en su página web registrándose antes (véase la figura que encabeza esta entrada).
La indexación de las celdillas se puede llevar a cabo mediante las llamadas curvas que rellenan el plano (space filling curves), que pasan por todas las celdllas de manera previsible y calculable, entre las que destaca la curva de Gosper, que pasa por una red de hexágonos:
En esta página puede verse todo un catálogo de estas curvas fractales.
Y por último, el contenido de cada celdilla puede ser una renderización, el valor de un atributo o incluso si es suficienemente pequeña, el vértice de una primitiva geométrica. Es posible que se puedan utilizar tanto para datos ráster como vectoriales.
¿Supone todo esto que estamos empezando a decir adiós a la proyecciones cartográficas clásicas de toda la vida? Es posible, no lo sabemos; el tiempo nos lo dirá.
Publicado por el editor.
otros sistemas rotan cada celdilla hexagonal al pasar de un nivel de resolución a otro:
como el que emplea la empresa canadiense PYXIS en la implementación que puede verse en su página web registrándose antes (véase la figura que encabeza esta entrada).
La indexación de las celdillas se puede llevar a cabo mediante las llamadas curvas que rellenan el plano (space filling curves), que pasan por todas las celdllas de manera previsible y calculable, entre las que destaca la curva de Gosper, que pasa por una red de hexágonos:
En esta página puede verse todo un catálogo de estas curvas fractales.
Y por último, el contenido de cada celdilla puede ser una renderización, el valor de un atributo o incluso si es suficienemente pequeña, el vértice de una primitiva geométrica. Es posible que se puedan utilizar tanto para datos ráster como vectoriales.
¿Supone todo esto que estamos empezando a decir adiós a la proyecciones cartográficas clásicas de toda la vida? Es posible, no lo sabemos; el tiempo nos lo dirá.
Publicado por el editor.


Comentarios